# 递归下降

先前用于描述的加减运算表达式的文法，实际上并不能直接通过递归下降分析法来解析。

说了这么多，递归下降到底是个什么玩意呢？
接下来我们通过以下能够应用递归下降进行解析的文法来解析输入串，了解其解析过程，读者大概就明白了。

ebnf
1
2
3
4
block = '{' {stat} '}'
stat = assignExp ';'
assignExp = ident '=' value
value = number | string

{stat} 表示重复 stat ，此处表示可以有 0~n 个 stat 。
其中， ident 是标识符， number 、 string 是字面量，我们都会放到词法分析中去解析，故不在此列出其文法。

首先，假设 block 输入串为：

plaintext
1
2
3
4
{
    a = 1;
    b = "qwq";
}

以下是解析的伪代码：

# 解析 block

plaintext
1
2
3
4
5
6
7
func ParseBlock(inStr) {
    inStr.match('{');
    while in.is('}') == false {
        ParseStat(in);
    }
    inStr.match('}');
}

首先从输入串中匹配 { 字符；
由于语句是可选的，因此需要检查紧接着的符号是否为 } 字符，不是的话就可以匹配 stat 了；
stat 是一个非终结符，需要继续展开，此处交给 ParseStat 进一步解析；
ParseStat 返回后，表示一条语句的解析完成了，但语句可能存在多条，因此循环进行；
最后匹配一个 } 字符；
block 解析完成。

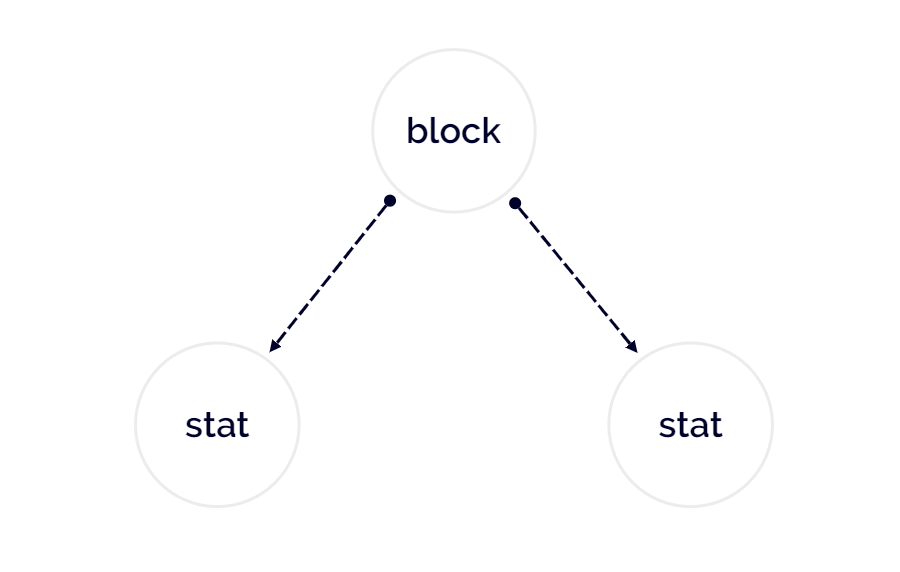
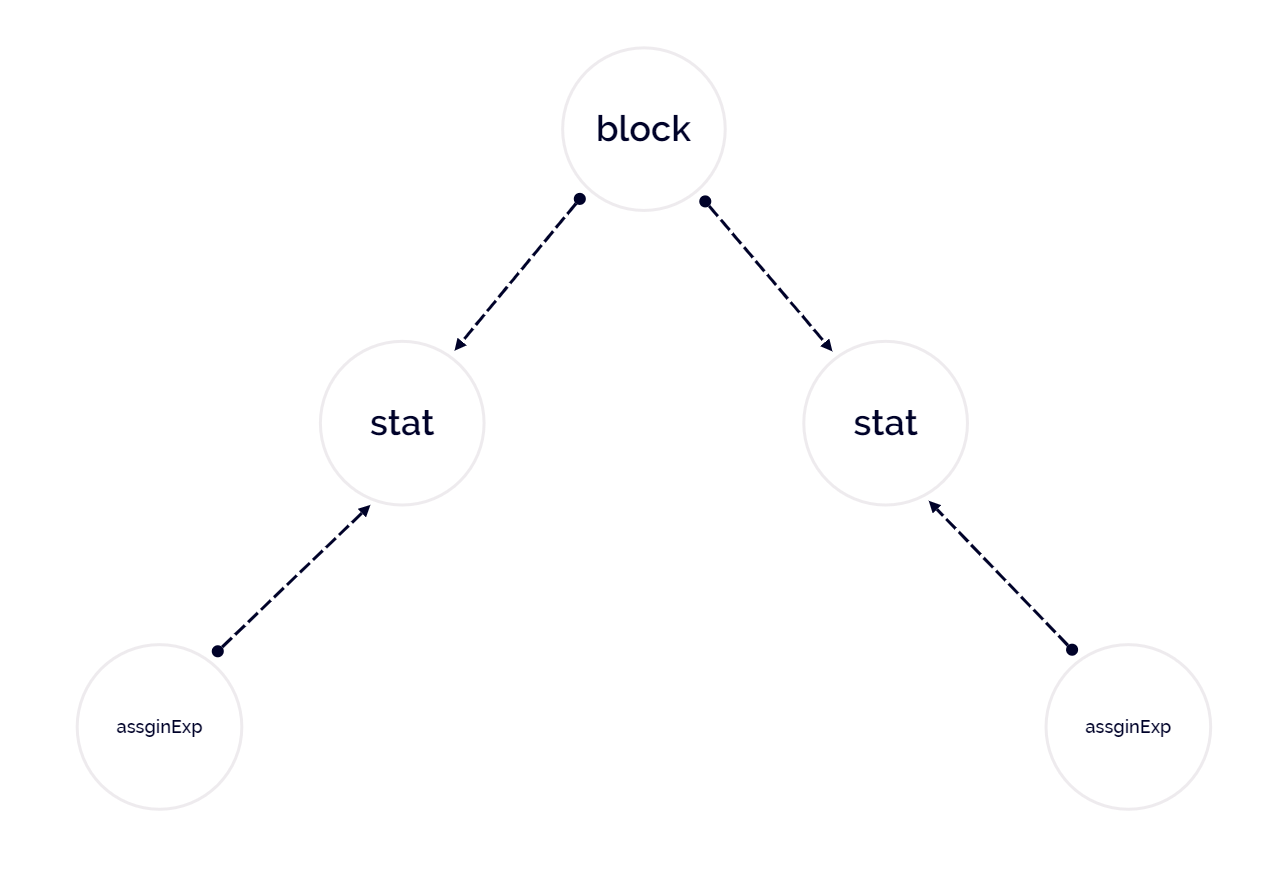
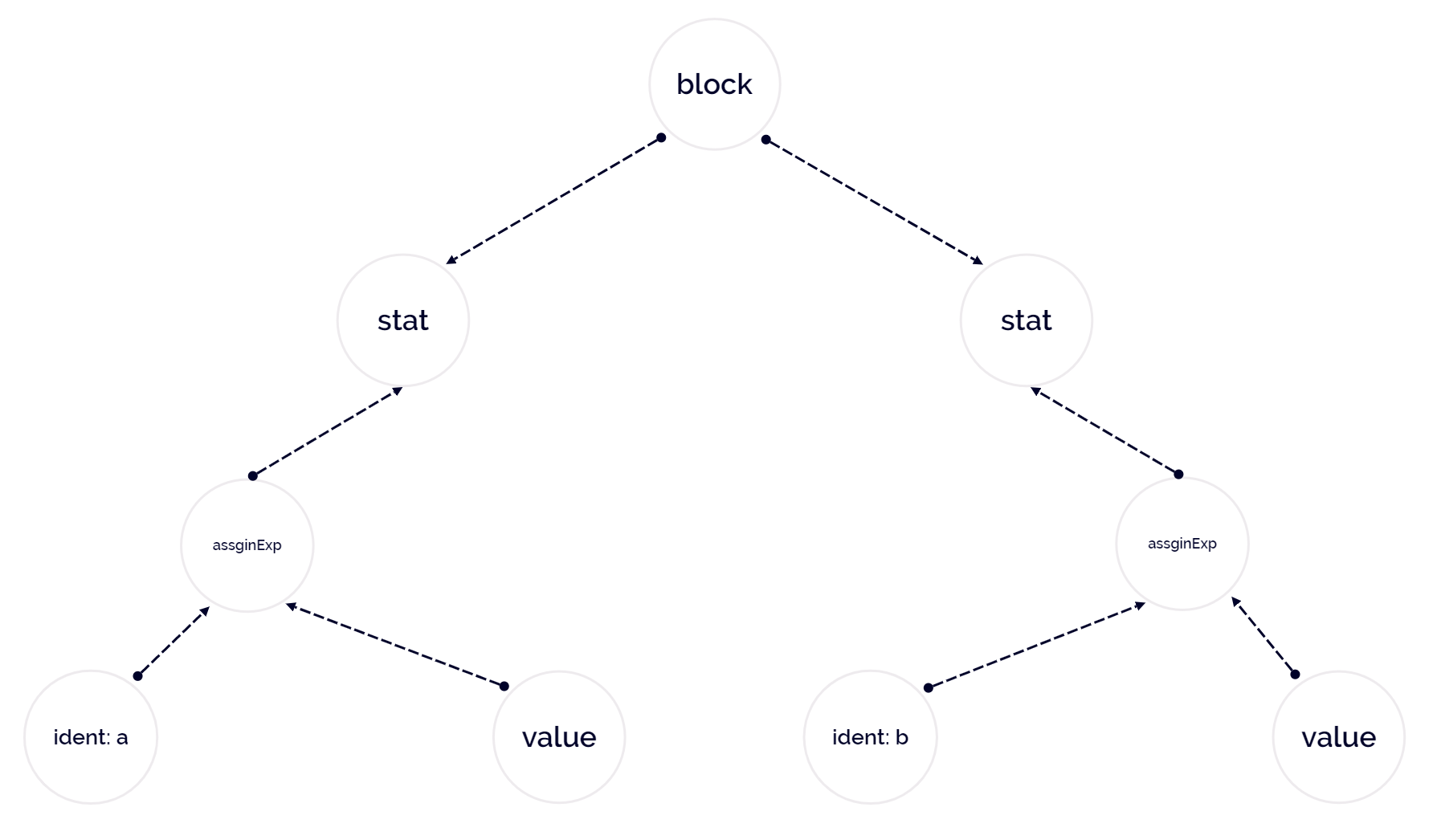
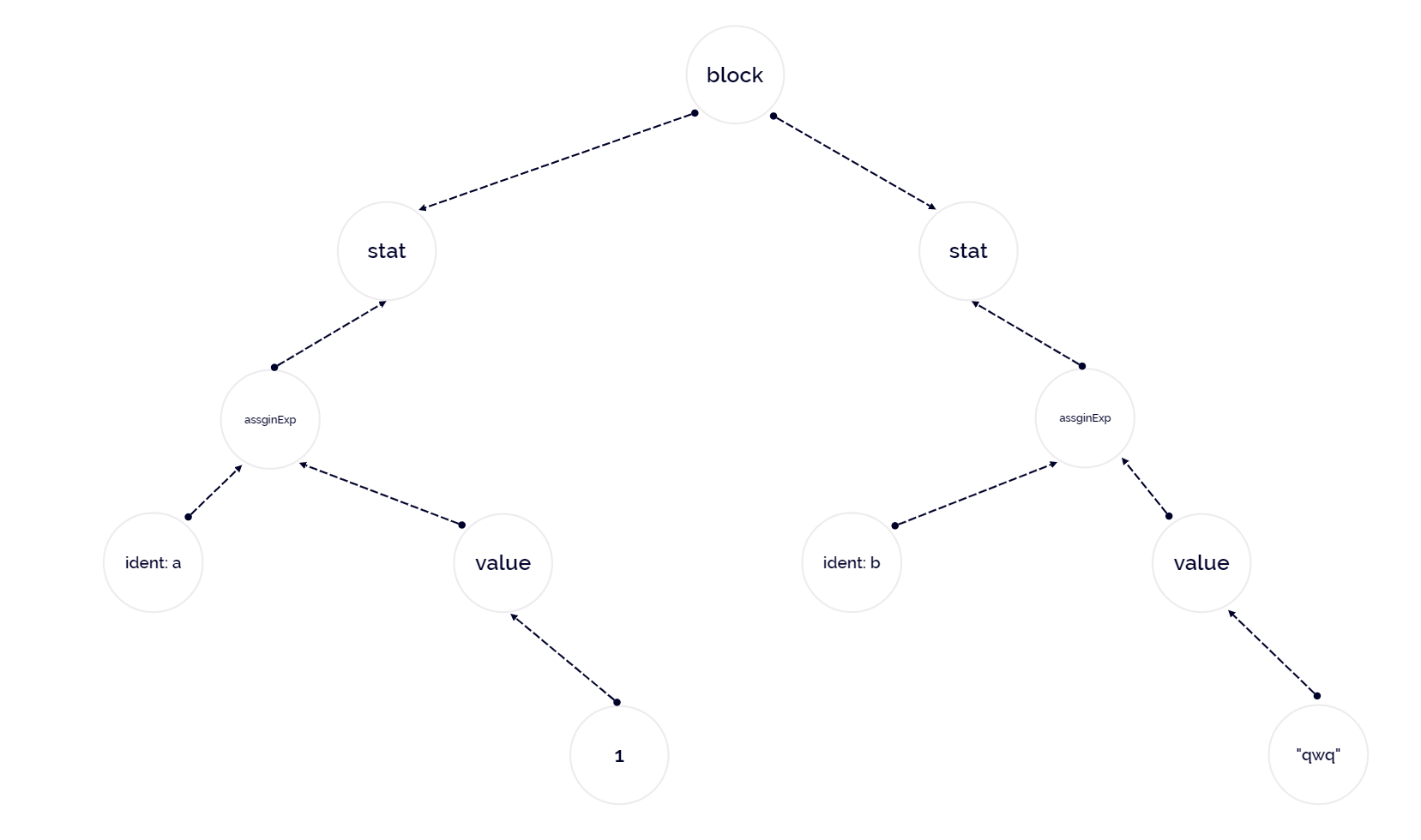
抽象语法树如下：

为什么这里没有添加 { 和 } 节点呢？
因为树构建完成后，我们自然可以知道这个节点是 block，在词法阶段的两个符号于语法树而言并无关紧要。

# 解析 stat

关于 stat 的解析，在 ParseStat 函数中完成：

plaintext
1
2
3
4
func ParseStat(inStr) {
    ParseAssignExp(inStr);
    inStr.match(';');
}

# 解析 assignExp

接下来是 assignExp ：

plaintext
1
2
3
4
5
func ParseAssignExp(inStr) {
    inStr.match(kIdent);
    inStr.match('=');
    ParseValue(inStr);
}

这里同样没有将符号 = 作为节点添加。

# 解析 Value

最后完成关于 Value 的解析：

plaintext
1
2
3
4
5
6
7
func ParseValue(inStr) {
    inStr in.is(kNumber) {
        in.match(kNumber);
        ret;
    }
    inStr.match(kString);
}

# 关键：描述文法

这种自顶逐层向下解析，以构造语法树的分析法，就叫做递归下降。
虽然笔者并没有在伪代码中添加构造树的节点相关的代码，但不妨碍读者理解递归下降。

你会发现，只要我们描述好了文法，用递归下降来解析输入串是一件非常简单的事情。

# 无限递进

还记得我在上一篇文章中所描述的文法吗？

如果直接编写解析代码，就会形成无限递进：

plaintext
1
2
3
4
5
6
7
8
9
10
func ParseExp(inStr) {
    ParseExp(inStr);
    if inStr.is('+') {
        inStr.match('+');
    }
    else {
        inStr.match('-');
    }
    ParseNumber(inStr);
}

# 左递归

如果非终结符 r 被直接或间接推导后，其结果最左边又出现非终结符 r 的情况，便称之为左递归。

理想解析情况：

plaintext
1
2
3
exp = exp + number
-> exp = number + number
...

代码解析情况：

plaintext
1
2
3
exp = exp + number
-> exp = exp + number + number
...

# 消除左递归

为此，我们需要改写文法，以避免出现左递归。

# 四则表达式文法

首先，我们用 EBNF 描述更加完整的四则表达式文法：

ebnf
1
2
3
4
5
exp = addexp
addexp = addexp oper2 mulexp | mulexp
oper2 = '+' | '-'
mulexp = mulexp oper1 number | number
oper1 = '*' | '/'

关于 number 的产生式就不再列出，实际上我们会在词法分析阶段将 number 解析为 token 。

我们现在很容易就能看出，在该文法中，左式为 addexp 和 mulexp 的产生式都存在左递归的问题。

如何消除呢？
首先观察产生式 addexp = addexp oper2 mulexp | mulexp
我们会发现这么一条规律：

  • addexp 的推导产生的句型，必然是 mulexp {oper2 mulexp}

于是我们可以重写文法为：

bnf
1
2
addexp ::= mulexp addexp'
addexp' ::= oper2 addexp' | ε

教学时消除左递归时经常用于举例的 BNF 文法；
其中 ε 表示空。
事实上关于 BNF 的格式规范，网上许多文章的写法似乎都不尽相同，在这里笔者也不做深究了。

ebnf
1
addexp = mulexp {oper2 mulexp}

使用 EBNF 描述的文法，通过 {} 做了简化。

事实上，我们如果直接按照第一种文法编写解析代码，最终构成的语法树会存在结合律的问题。
如果使用第二种文法，以多叉树的形式存储其节点，则会更加简单，因此本系列文章采用第二种文法。

# 构造语法树

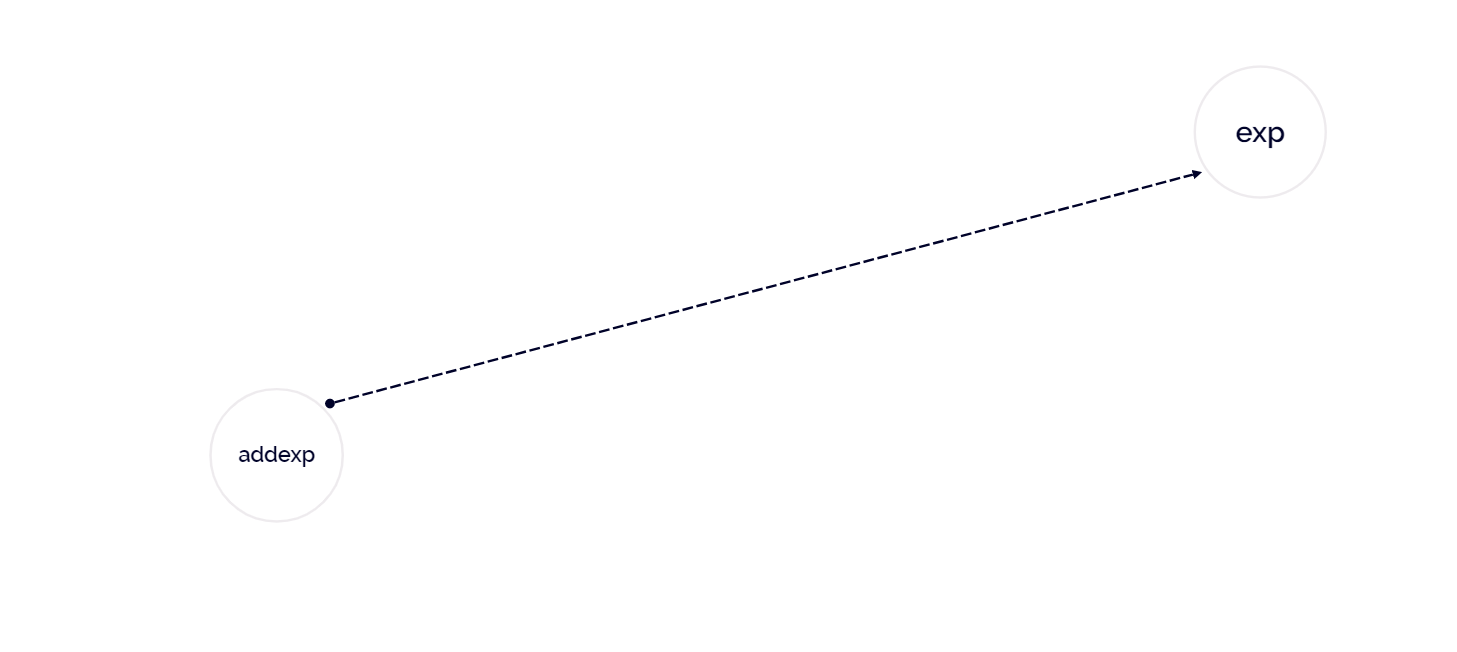
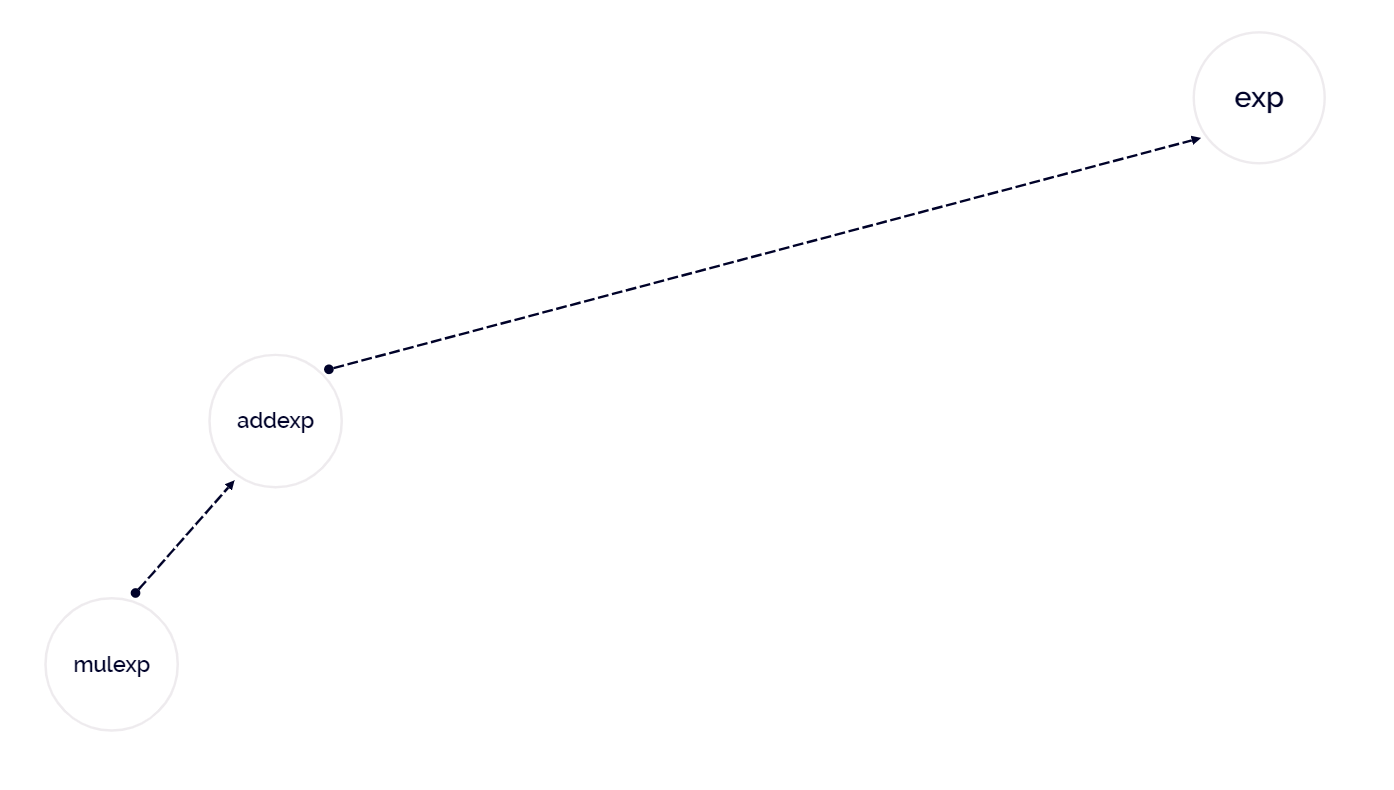
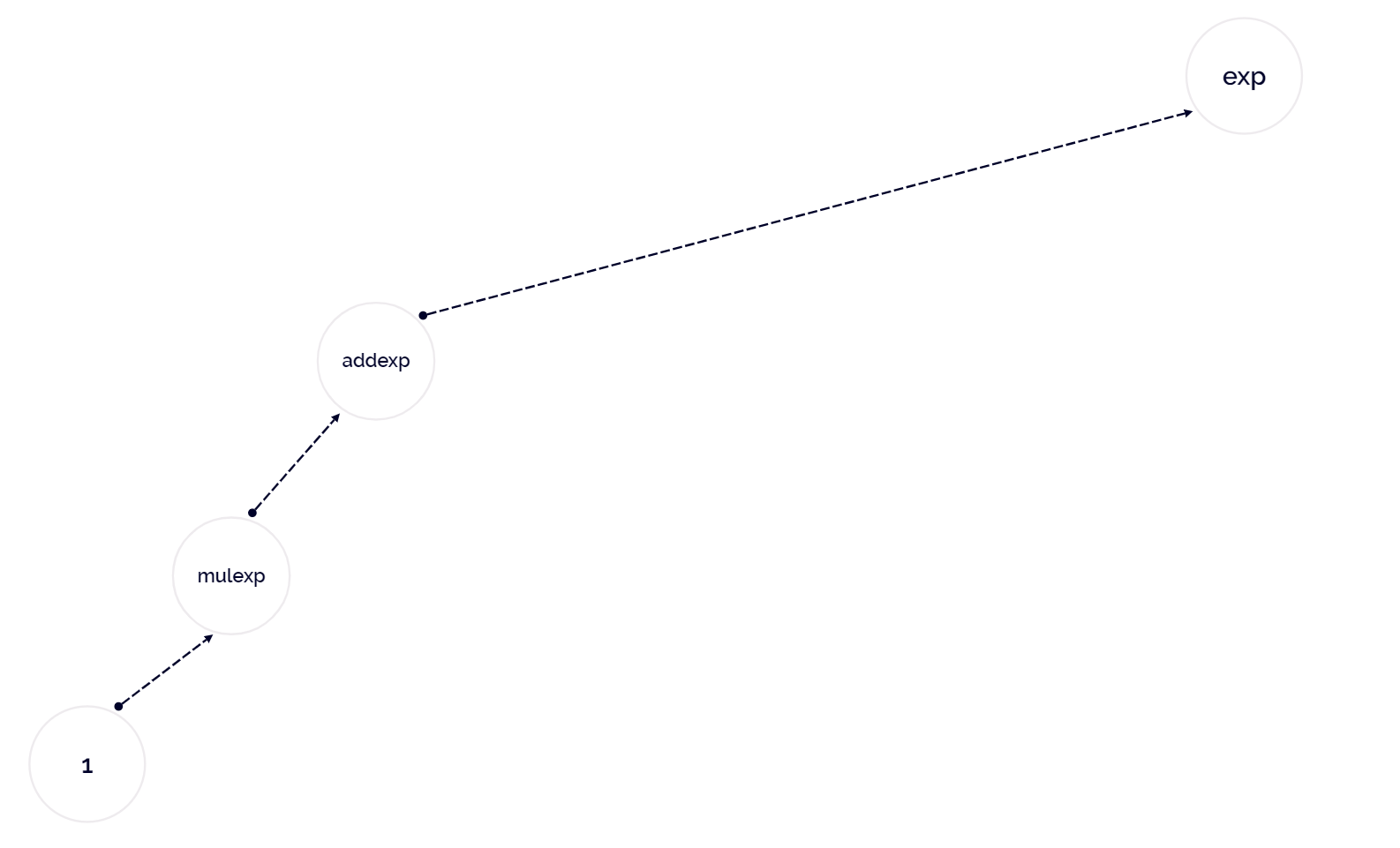
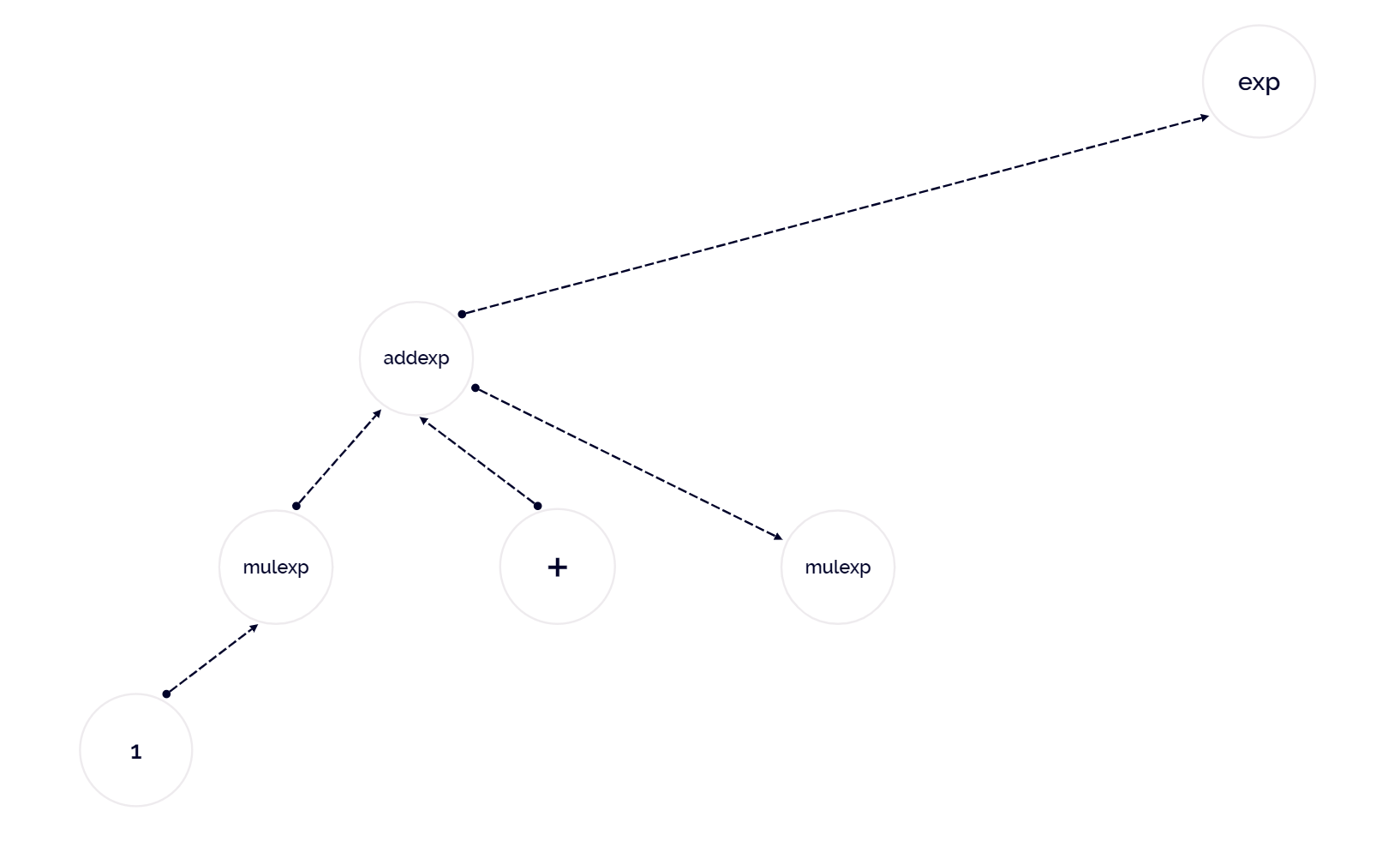
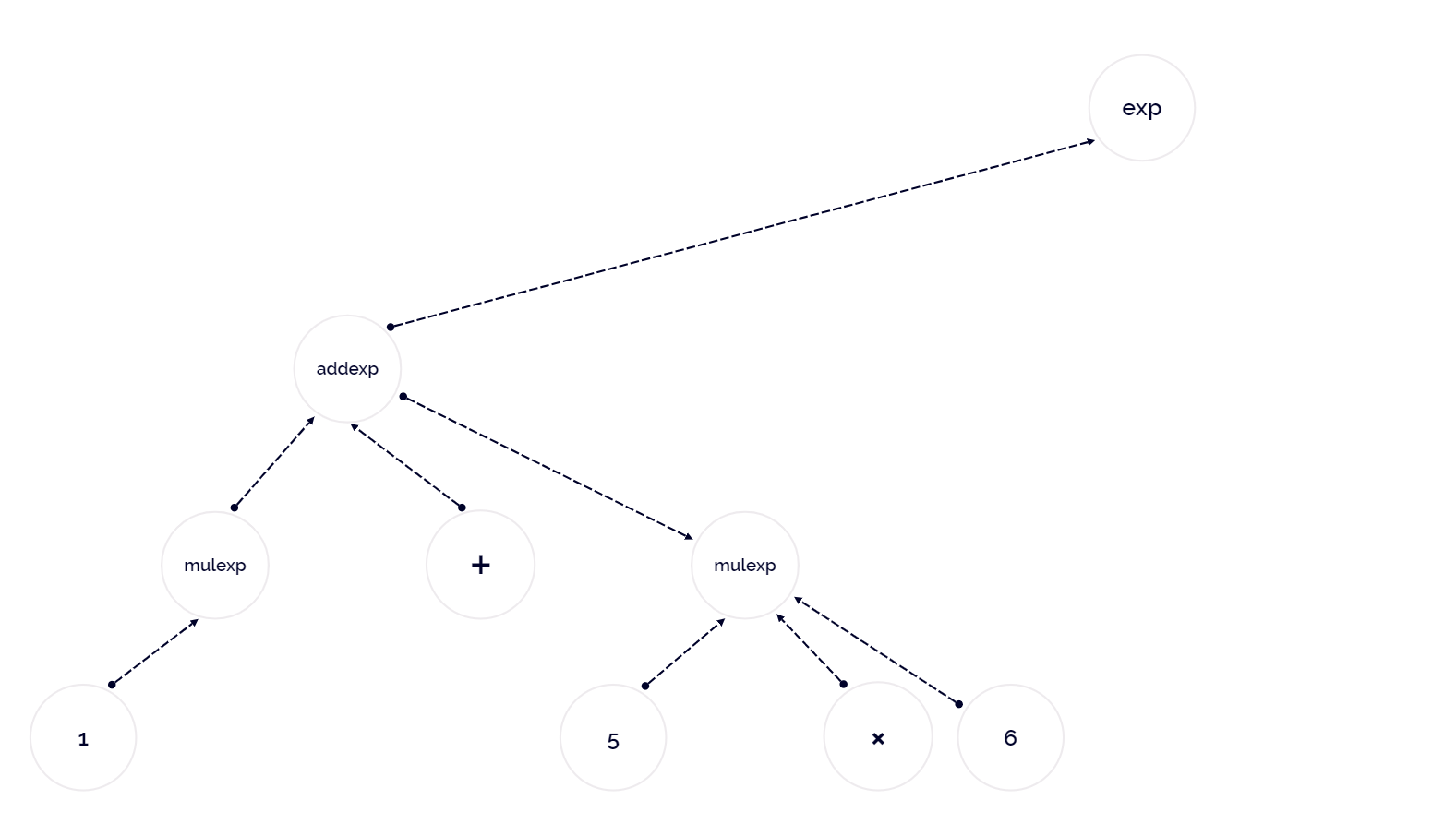
接下来我们尝试基于此文法与表达式 1 + 5 * 6 ，构造其抽象语法树。

以下是完整文法：

ebnf
1
2
3
4
5
exp = addexp
addexp = mulexp {oper2 mulexp}
oper2 = '+' | '-'
mulexp = number {oper1 number}
oper1 = '*' | '/'

以下是解析过程：

读者不妨尝试自己编写一些表达式，然后画一画解析图，找找感觉。
也可以尝试自己在脑中遍历这颗语法树，看看能否能够正确计算出结果。

# 参考文献

[1] 消除左递归.https://blog.csdn.net/qq2071114140/article/details/102787831