# 由此开始

如果你曾经接触过《编译原理》的话，不知道是否与我有着同样的困惑呢？

各种不近人情的名词，公式乱飞，这让我学习起来格外痛苦。

我在阅读过不少文章、书籍，并且尝试敲下一些代码之后，才逐渐理解了一些较为关键的东西。

实际上，当我真正完成了对四则运算表达式的解析的那一刻，我才真切感受到了编译原理的优雅与美妙之处，这大概就是由人类智慧的伟大之处吧 (偏得有点远了)。

因此，我才会选择先从四则运算表达式开始，将其逐步扩展成为一门 通用编程语言 ，也能让读者每一节都能感受到学习有所反馈的喜悦。

# 初尝构思

现在，我来尝试给你出一道题吧，请你用你所熟悉的语言，编写一个模块：

  1. 输入符合四则运算表达式规范的字符串 (可以假定只有整数，不存在括号)；
  2. 输出整型结果；
  3. 要求关键逻辑由自己实现，不可借由库、语言本身提供的功能。

你能实现吗？

是否觉得脑子有些空白，难以组织成较为优雅的实现思路呢？

如果你现在就能想到很棒的解法，那至少你要比我厉害多了。

我曾经因为某些需求做过尝试，虽然最后写出来了，但是具体实现也非常丑陋，这里就不献丑了。

但是我可以给你大致描述一下我当初的思路：

  • 首先，查找字符串中优先级较高的运算符 * / ，再前 / 后瞻运算符前后的数字，这个子串也能形成一个表达式；

  • 算出结果后，在原表达式中，用结果替换掉子串 (刚刚被计算的表达式)，再继续查找。

  • 完成后再从头开始查找优先级更低一级的运算符 + - ，直到运算完成。

当然，我们不会用这么低效的方法，也不会要求现在就给出实现。

现在提出这个问题，并不是为了为难你，只是为了让你记住眼下的感觉，当你学完本系列文章后，再回来看看，这一道题，是否真的有那么难呢？

# 抽象语法树

咱们先来看百度百科对 抽象语法树 的定义：

在计算机科学中，抽象语法树（Abstract Syntax Tree，AST），或简称语法树（Syntax tree），是源代码语法结构的一种抽象表示。它以树状的形式表现编程语言的语法结构，树上的每个节点都表示源代码中的一种结构。

嗯… 不愧是名字就带着抽象的东西，连说明都这么抽象。

咱们先不整那么多虚头巴脑的，干就完了。

# 构造四则运算表达式的 AST

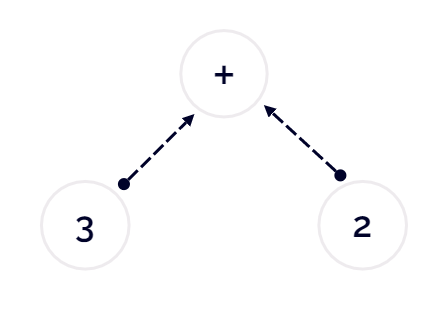
3 + 2

这个是大家熟悉的算术表达式，实际上，我们的大脑是如何计算这个表达式的呢？当然需要遵循某些规则：

  1. 先乘除
  2. 再加减
  3. 从左往右结合

那我们自然是需要先左往右找在表达式中找到 * 、 / 两种符号，好消息是，没有，嘿嘿。

接下来继续左往右找 + 、 - ，找到之后将其取出，这也是我们需要计算的子表达式。

我们将其分成三部分，分别是：

  • 左边的数字 3
  • 加法运算符 +
  • 右边的数字 2

人脑的表达式计算模型，可以归纳成这么一颗树型结构：

遍历树与我们的计算过程极度相似：

  1. 根节点，是加法，表明需要将左子节点与右子节点相加；
  2. 3 + 2 ，返回结果 5 ；
  3. 遍历结束；

# 多运算符与结合律

那么，当一个表达式中，存在多个运算符时，应该如何构造语法树呢？
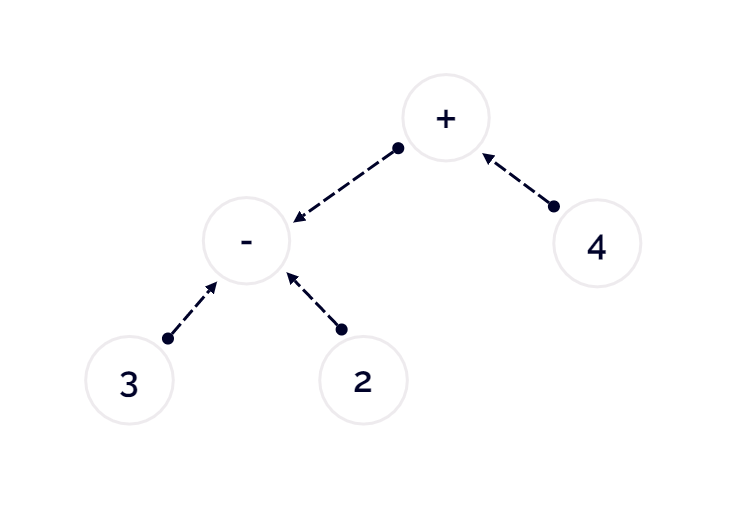
接下来我们构造表达式 3 - 2 + 4 的树。

首先我们应该注意的一点是，需要先被执行运算 (优先级更高) 的子表达式，其节点的相对深度更深：

还是先来遍历这颗树：

  1. 根节点，是加法，表明需要将左子节点与右子节点相加；
    1. 左子节点是减法，表明需要用左子节点减去右子节点，需要继续向下展开；
    2. 3 - 2 ，返回结果 1 ；
  2. 1 + 4 ，返回结果 5 ；
  3. 遍历结束；

因此，遍历的过程也符合我们所要求的 左结合律 。

  • 由左边的运算符开始，向右结合。
  • 同优先级下，我们需要优先计算左边的运算符组成的子表达式，

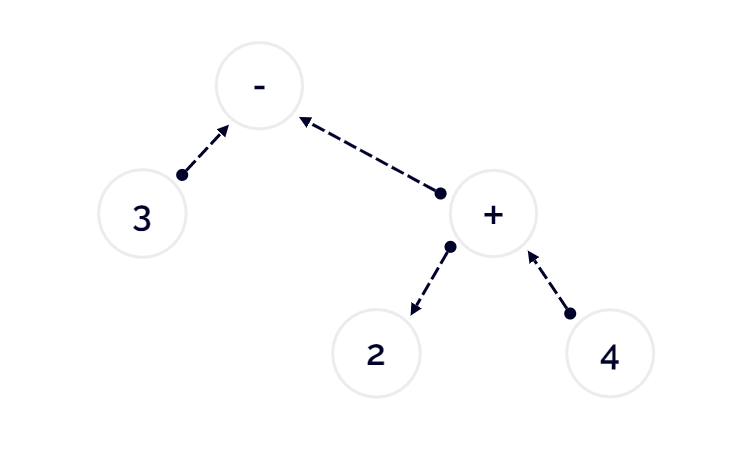
接下来我再给你画一下另一种情况，你也就明白了。

你可以尝试一下遍历这棵树，会发现先被执行的一定是加法，这并不符合我们的从一开始就要求的 左结合律 。
在部分情况下，由于结合律的错误，就会产出错误的结果：

  • 如我们本次求解的表达式，通过遍历此树得出的结果为 -3 。

# 目标：根据语法规则生成 AST

我不说你大概也已经猜到了，其实我们上面所构造的树，在当前的应用场景下，就叫做 抽象语法树 。

遍历抽象语法树并计算的过程，与我们人脑对表达式的计算的过程是十分相似的。

也就是说，我们只需要构造出这么一颗抽象语法树，就已经基本上完成了编译工作的一大半。
此时，若需要执行编译产生的结果，只需要遍历我们所生成 AST 即可。

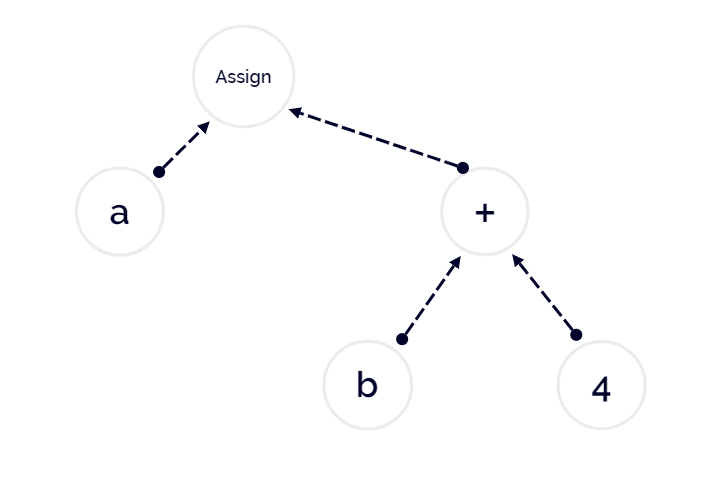
如下图：

在遍历的过程中，我们就能够正确的完成对加法表达式的加法运算，再完成对赋值表达式的赋值运算。

# AST 解释器

最后，笔者向读者展示了有关 "解释器" 的东西，是的，即便你难以置信。
遍历这棵树的过程，就可以叫做解释；
如果我们写出代码实现遍历树的过程，即是 AST解释器 。

当然，解释器是一种比较广泛的概念，即便到后面我们基于 AST 生成了字节码，交给虚拟机执行，我们的程序也依然可以称之为解释器，只不过解释的对象从 AST 换成了字节码。

我个人觉得，当初造这个词的人只是为了区分所谓的 "编译型语言" 和 "解释型语言"。
以下是百度百科对解释器的定义：

解释器（英语：Interpreter），又译为直译器，是一种电脑程序，能够把高级编程语言一行一行直接转译运行。解释器不会一次把整个程序转译出来，只像一位 “中间人”，每次运行程序时都要先转成另一种语言再作运行，因此解释器的程序运行速度比较缓慢。它每转译一行程序叙述就立刻运行，然后再转译下一行，再运行，如此不停地进行下去。

  • 此处关于 每转译一行程序叙述就立刻运行 的说明也不尽然，至少现在很多被称为 解释器 的程序，并非如此 (如 Python 解释器、Java 解释器等)。